At the American Economic Association, the paper Credit, Financial Conditions, and Monetary Policy Transmission (the "preview" PDF, 39 pages) by David Aikman of the Bank of England, and Andreas Lehnert, Nellie Liang, and Michelle Modugno of the Federal Reserve Board. There is a lot of good stuff here.
The complete abstract:
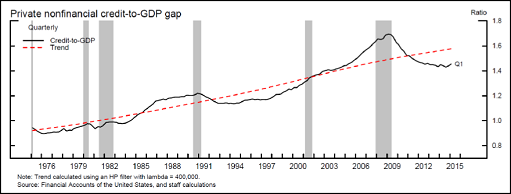
We show that the effects of financial conditions and monetary policy on U.S. economic performance depend nonlinearly on nonfinancial sector credit. When credit is below its trend, an impulse to financial conditions leads to improved economic performance and monetary policy transmission works as expected. By contrast, when credit is above trend, a similar impulse leads to an economic expansion in the near-term, but then a recession in later quarters. In addition, tighter monetary policy does not lead to tighter financial conditions when credit is above trend and is ineffective at slowing the economy, consistent with evidence of an attenuated transmission of policy changes to distant forward Treasury rates in high-credit periods. These results suggest that credit is an important conditioning variable for the effects of financial variables on macroeconomic performance.
I love it. That first sentence is almost haiku:
the effects of financial conditions and monetary policy
on U.S. economic performance
depend nonlinearly on nonfinancial sector credit.
on U.S. economic performance
depend nonlinearly on nonfinancial sector credit.
Well okay, not haiku. But I like what they have to say. Remember Keynes saying the classical theory is a "special case" of his general theory? This is like that. When credit is below trend, the economy "works as expected." But when credit is above trend, things go haywire. Credit below trend is the special case. Above trend is where we are now. Above trend is where we've been since... well, for decades and decades. I was going to say "since World War One" but you probably wouldn't buy that.
Economists are seeking another general theory. They struggle to understand how the economy operates in a high-debt environment. That's what the AEA paper is, an attempt to understand how the economy works under conditions of "excess credit".
I offer the short answer: Under conditions of excess credit, the economy doesn't work. Under conditions of excess credit, civilization evolves away from its "capitalism and democracy" phase, toward whatever comes next.
 |
| From The Lessons of History by Will and Ariel Durant |
There has always been trade. There is always this force at work, concentrating wealth. And here's the thing: When wealth grows faster than it concentrates, wealth spreads. You get the upswing of an economic cycle. But when wealth concentrates faster than it grows, you get the downswing.
Civilization is just a massive business cycle. Capitalism is just a phase of it. If you want to stay in the capitalist phase, you have to limit the concentration and encourage the distribution of wealth to suit that phase of the cycle. This is the new general theory economists are looking for. I hope they find it before it's too late.